Breadcrumb

Physical characterization of Cu2ZnGeSe4thin films from annealing of Cu-Zn-Ge precursor layers
Cu2ZnGeSe4(CZGeSe) can be considered as a potential alternative for wide band gap thin film devices. In this work, CZGeSe thin films were deposited on Mo-coated soda lime glass substrates by sequential deposition of sputtered Cu, Zn and e-beam evaporated Ge layers from elemental targets followed by annealing at high temperature using H2Se gas. We report on the effect of the precursor stack order and composition and the impact of the annealing temperature on the physical properties of CZGeSe thin films. The optimal layer morphology was obtained when using a Mo/Cu/Zn/Ge precursor stack annealed
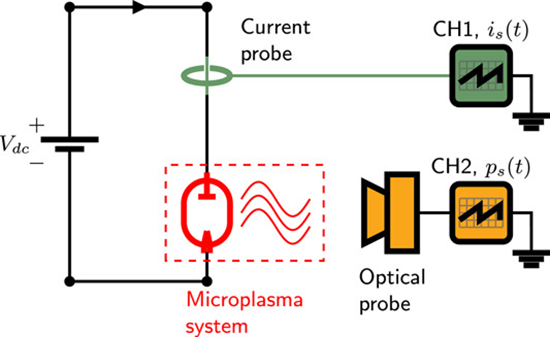
Parallel random bitstreams from a single source of entropy based on nonthermal electrochemical microplasma
This study presents the simultaneous generation of two uncorrelated and continuous high-quality random bitstreams originating from a single physical system based on confined, nonthermal electrochemical microplasma operating under atmospheric conditions. The randomness is intrinsically inherited from the time-resolved electrical current and optical emission intensities of the microplasma system, which were collected using wide bandwidth current probe and photodetection device. The parallel bitstreams pass unambiguously all 15 NIST SP 800-22 statistical tests without the need for any data post

A collection of interdisciplinary applications of fractional-order circuits
An attractive feature of fractional calculus is its application in various interdisciplinary fields, extending from biomedical and biological notions to mechanical properties. For their description, fractional-order models have outperformed the corresponding integer-order models, resulting in a more realistic behavior, due to the additional degrees of freedom offered and the long-term memory effect that reflects the fractional order. These improved features are processed by appropriate circuit implementations, derived through several approximation methods, whose primary objective is to provide
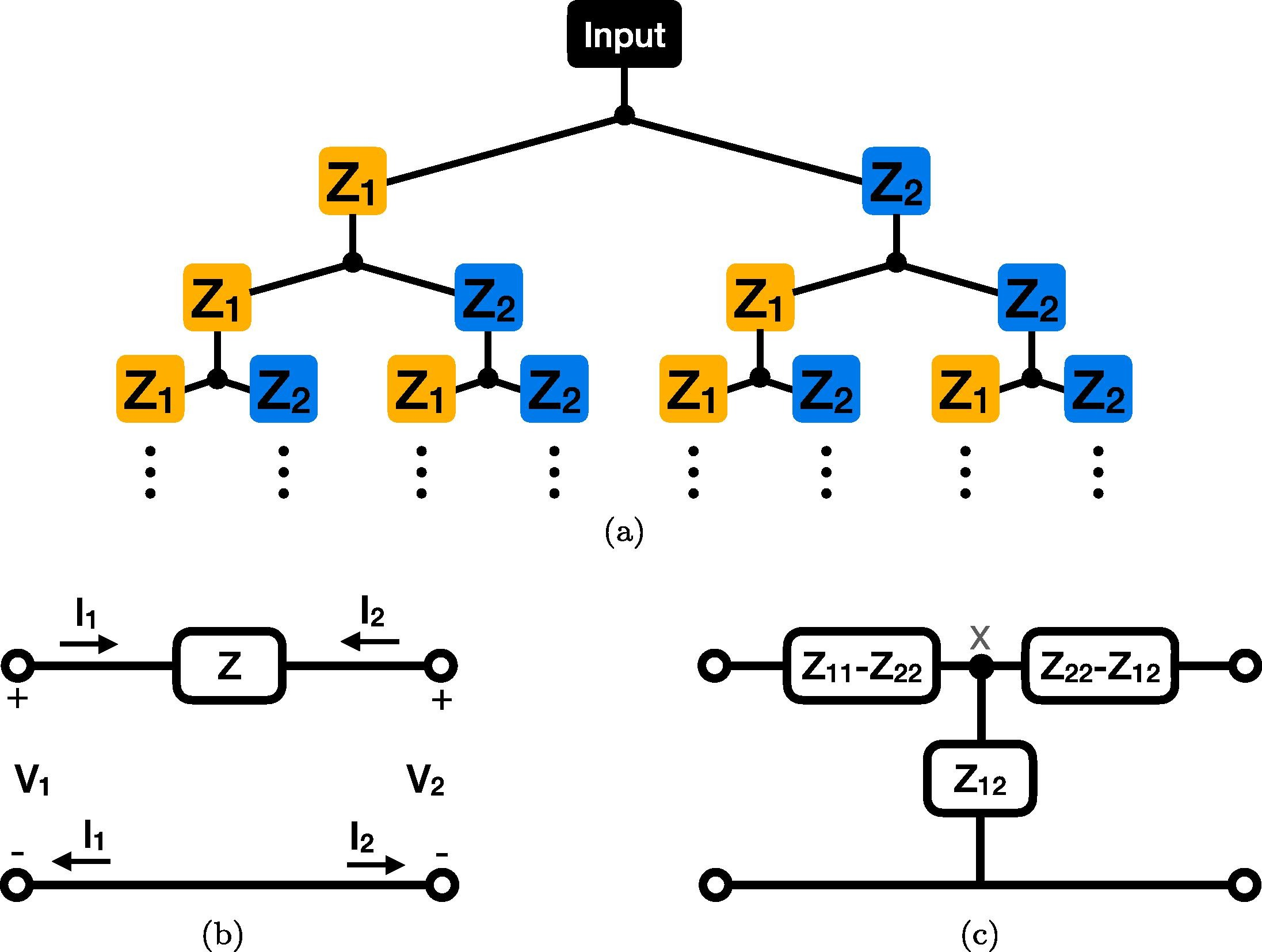
Generalizing the Warburg impedance to a Warburg impedance matrix
We seek to generalize and study the well-known Warburg impedance element, which has an impedance proportional to 1/s (s=jω is the complex frequency), to a two-port impedance network. For this purpose, we consider an infinite binary tree structure inside which each impedance is treated as a two-port network. We obtain a Warburg impedance matrix, which is both symmetrical and reciprocal, and study its equivalent circuit behavior. Interestingly, the equivalent circuit contains two resistors and a Cole–Davidson type impedance proportional to 1+2/(τs), where τ is a time constant. Simulation results
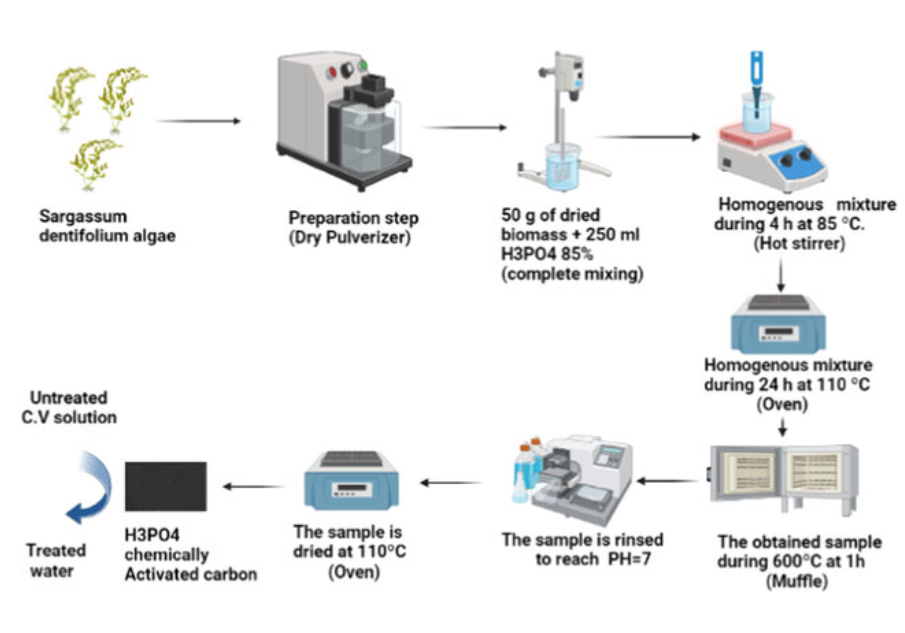
Crystal violet removal using algae-based activated carbon and its composites with bimetallic Fe0-Cu
The textile industry is considered a source of pollution because of the discharge of dye wastewater. The dye wastewater effluent has a significant impact on the aquatic environment. According to the World Bank, textile dyeing, and treatment contribute 17 to 20% of the pollution of water. This paper aims to prepare the bimetallic nano zero-valent iron-copper (Fe0-Cu), algae-activated carbon, and their composites (AC-Fe0-Cu), which are employed as adsorbents. In this paper, Synthetic adsorbents are prepared and examined for the adsorption and removal of soluble cationic crystal violet (CV) dye
MOS realizations of fractional-order elements
The exploitation of fractional calculus in engineering applications requires the utilization of fractional-order elements. As there is no immediate access to such type of elements, emulators that proportionally imitate their behavior are developed. The realization of emulators of fractional-order elements is based on the approximation of their impedance function. Subsequently, an advantageous option for the circuit implementation of the obtained, approximated impedance function is MOS transistor-based configurations, as they provide a dynamic system with electronically adjustable parameters
Robust adaptive supervisory fractional order controller for optimal energy management in wind turbine with battery storage
To address the challenges of poor grid stability, intermittency of wind speed, lack of decision-making, and low economic benefits, many countries have set strict grid codes that wind power generators must accomplish. One of the major factors that can increase the efficiency of wind turbines (WTs) is the simultaneous control of the different parts in several operating area. A high performance controller can significantly increase the amount and quality of energy that can be captured from wind. The main problem associated with control design in wind generator is the presence of asymmetric in the
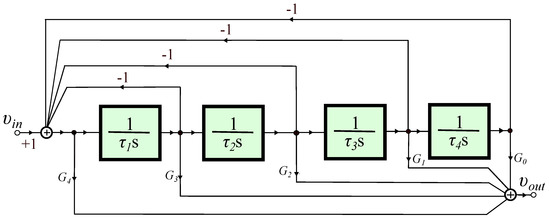
A 1 + α Order Generalized Butterworth Filter Structure and Its Field Programmable Analog Array Implementation
Fractional-order Butterworth filters of order 1 + (Formula presented.) (0
Di- and tri- cyclic aromatic hydrocarbons removal using different prepared materials based Sargassum dentifolium algae, and iron oxide
Polycyclic aromatic hydrocarbons (PAHs) are highly toxic and carcinogenic compounds as they are low water solubility, hardly degradable and may persist in the environment for many years. Therefore, this study was directed to PAHs ‘anthracene and naphthalene’ removal using a combination method between adsorption and degradation using sunlight. Three adsorbent materials, iron oxide (Fe) alone, Sargassum dentifolium (S) alone, and mixture of Iron oxide and Sargassum dentifolium (FeS) were prepared. Afterwards, optimisation process was performed for the three adsorbent forms through some

Fractional-order inverse filters revisited: Equivalence with fractional-order controllers
The equivalence of fractional-order inverse filters with fractional-order controllers is demonstrated in this work. This is achieved by appropriately rewriting the filters transfer functions in order to clarify the correspondence between the gain and time-constant of the filters and the scaling factor and differentiation/integration constant of the controllers. Possible implementations of fractional-order inverse filters using second generation voltage conveyors are presented and an application example, related to the control of a motion system, is demonstrated for evaluating the behavior of
Pagination
- Previous page ‹‹
- Page 2
- Next page ››
