Breadcrumb

Modified Blowfish Algorithm Based on Improved Lorenz Attractor
Image security becomes important topic because of increasing image usage in communication besides assures information security which is unseen in these images such as military and medical images. Blowfish is a superb symmetric cryptography that ensures a high degree of resistance to attacks. The proposed system modifies Blowfish algorithm by substituting the function in blowfish round with light weight function to save memory and resources of the platforms and Using 3-D chaotic system (Improved Lorenz) that work as a key timetable for creating Blowfish sub keys in order to increasing
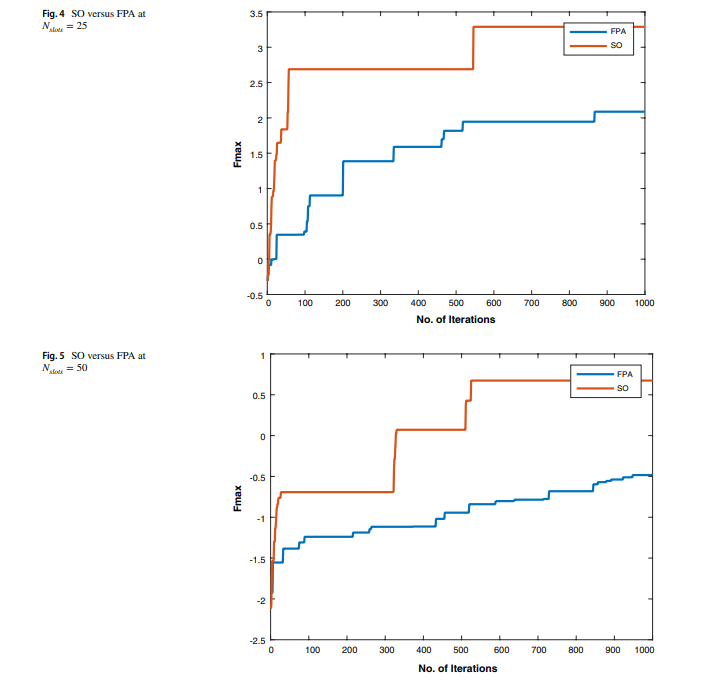
A power-aware task scheduler for energy harvesting-based wearable biomedical systems using snake optimizer
There is an increasing interest in energy harvesting for wearable biomedical devices. This requires power conservation and management to ensure long-term and steady operation. Hence, task scheduling algorithms will be used throughout this work to provide a reliable solution to minimize energy consumption while considering the system operation constraints. This study proposes a novel power-aware task scheduler to manage system operations. For example, we used the scheduler to handle system operations, including heart rate and temperature sensors. Two optimization techniques have been used to

Mathematical Techniques of Fractional Order Systems
Mathematical Techniques of Fractional Order Systems illustrates advances in linear and nonlinear fractional-order systems relating to many interdisciplinary applications, including biomedical, control, circuits, electromagnetics and security. The book covers the mathematical background and literature survey of fractional-order calculus and generalized fractional-order circuit theorems from different perspectives in design, analysis and realizations, nonlinear fractional-order circuits and systems, the fractional-order memristive circuits and systems in design, analysis, emulators, simulation

Interdigitated C-Patch Metamaterial Antenna for Terahertz Sensing
This paper proposes a metamaterial Terahertz sensor with detected sensitivity for biomedical applications. The proposed sensor consists of two interdigitated golden C-shaped structures on top of Teflon substrate that is backed by a gold layer. The absorption spectrum contains a peak resonance corresponding to the maximum absorption of the sensor. The proposed sensor has a maximum narrow-band absorption at 3.35 THz, with an average sensitivity of 2.256 THz/RIU and a quality factor of 22.3. The developed model is checked for the range of refractive index range between n= 1.3 to n= 1.4 to check

Energy Harvesting Management Unit for Wearable Devices
Energy harvesting materials and systems have become a popular study topic that is rapidly expanding. The harvesters will be used for a variety of applications, including distributed wireless sensor nodes for structural health monitoring, embedded and implanted sensor nodes for medical applications, recharging large system batteries, monitoring pressure in automobiles, powering unmanned vehicles, and running security systems in domestic settings. Components and devices at micro-macro sizes, spanning materials, electronics, and integration, have recently been developed. Energy harvesting has

Wastewater Treatment: Recycling, Management, and Valorization of Industrial Solid Wastes
Wastewater Treatment: Recycling, Management, and Valorization of Industrial Solid Wastes bridges the gap between the theory and applications of wastewater treatments, principles of diffusion, and the mechanism of biological and industrial treatment processes. It presents the practical applications that illustrate the treatment of several types of data, providing an overview of the characterization and treatment of wastewaters, and then examining the different biomaterials and methods for the evaluation of the treatment of biological wastewaters. Further, it considers the various types of

Indoor Air Quality Monitoring Systems for Sustainable Medical Rooms and Enhanced Life Quality
Indoor air pollution poses a substantial risk to human health and well-being, underscoring the crucial requirement for efficient monitoring systems. This paper introduces an advanced Air Pollution Monitoring System (APMS) tailored explicitly for indoor settings. The APMS integrates sensors and a user interface, ensuring the delivery of real-time and precise data concerning air quality parameters such as particulate matter (PM), volatile organic compounds (VOCs), carbon dioxide (CO2), as well as temperature and humidity. The proposed APMS has several advantages, including low maintenance

IOT-based air quality monitoring system for agriculture
Air quality assessment has been discussed for urban environments with a high degree of industrialization, as they are infested with hazardous chemicals and airborne pollutants. The assessment is carried out by monitoring stations, that basically support limited areas while leaving large geographical areas uncovered. The expansion in the agriculture sector directed us towards air quality assessment on the farms. This is because research has shown that crops can be injured when exposed to high concentrations of various air pollutants, while also affecting farmers' health states. But those air

A Robust Deep Learning Detection Approach for Retinopathy of Prematurity
Retinal retinopathy of prematurity (ROP), an abnormal blood vessel formation, can occur in a baby who was born early or with a low birth weight. It is one of the primary causes of newborn blindness globally. Early detection of ROP is critical for slowing and stopping the progression of ROP-related vision impairment which leads to blindness. ROP is a relatively unknown condition, even among medical professionals. Due to this, the dataset for ROP is infrequently accessible and typically extremely unbalanced in terms of the ratio of negative to positive images and the ratio of each stage of it
Applications of continuous-time fractional order chaotic systems
The study of nonlinear systems and chaos is of great importance to science and engineering mainly because real systems are inherently nonlinear and linearization is only valid near the operating point. The interest in chaos was increased when Lorenz accidentally discovered the sensitivity to initial condition during his simulation work on weather prediction. When a nonlinear system is exhibiting deterministic chaos, it is very difficult to predict its response under external disturbances. This behavior is a double-edged weapon. From a control and synchronization point of view, this proposes a
Pagination
- Previous page ‹‹
- Page 2
- Next page ››
