Breadcrumb

Bowtie-Shaped Plasmonic Nanoparticles-Enhanced Photovoltaic Anti-Reflective Coating
Light trapping is a promising technique that enhances sunlight absorption by solar cells. This paper presents a study of bow-tie-shaped nanoparticles embedded in the antireflection coating of photovoltaic solar cells, which enhances the optical transmission of the photovoltaic surface. Therefore, the optical path length for light penetration is increased through the semiconductor active layer. First, the fundamental electric field modes of a single nanoscaled bow-tie are examined under excitation of plane waves with different polarizations. Second, an array of bow-tie-shaped nanoparticles is

Different Approximation Techniques For A FOPID Feedback Control of a DC Motor
DC motors are commonly employed in many industrial applications due to their various advantages. This study aims to compare the response of the Oustaloup-Recursive-Approximation (ORA) and El-Khazali's approximation method in controlling a DC motor with a FOPID controller. The two employed methods are used to design the FOPID and approximate. For various fractional orders, many behaviours are presented. A simulation comparison between these methods is performed regarding overshoot, settling time and rise time. © 2022 IEEE.
Quasi-Monte Carlo Technique With the Halton Sequence Applied To Mushroomwaveguide Photodetectors (WGPDs)
Monte Carlo (MC) simulation is a widely adopted computational method that relies on random sampling, but it is susceptible to exhibiting patterns and biases due to the use of pseudo-random numbers. In contrast, Quasi-Monte Carlo (QMC) techniques employ low discrepancy sequences, resulting in more evenly distributed random numbers and the potential for more accurate and reliable simulation outcomes. Mushroom-Waveguide Photodetectors (WGPDs) are integrated to a wide range of applications, and their performance is critically dependent on precise dimensional parameters. In this research, we

Hardware Realization of High-Speed Area-Efficient Floating Point Arithmetic Unit on FPGA
Floating point representations are required in many applications due to their universality and ability to represent huge numbers accurately and in compact bit-width. Floating point arithmetic is complex, performance inefficient, and area-consuming compared to integer arithmetic operations. In this paper, hardware realization of area-efficient high-performance floating point arithmetic units for IEEE 754 floating point single precision and double precision formats on FPGA are proposed. The proposed units achieved the same accuracy as software in all tested cases and were able to produce the
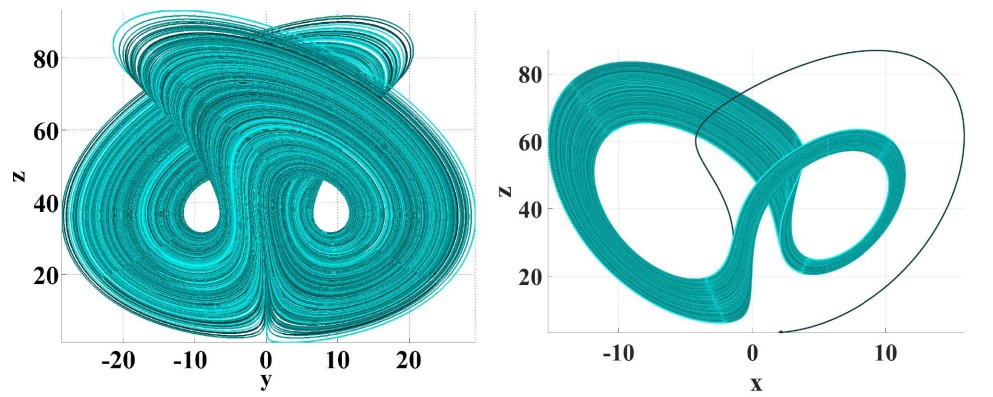
Chaotic Dynamics and FPGA Implementation of a Fractional-Order Chaotic System with Time Delay
This article proposes a numerical solution approach and Field Programmable Gate Array implementation of a delayed fractional-order system. The proposed method is amenable to a sufficiently efficient hardware realization. The system's numerical solution and hardware realization have two requirements. First, the delay terms are implemented by employing LookUp Tables to keep the already required delayed samples in the dynamical equations. Second, the fractional derivative is numerically approximated using Grünwald-Letnikov approximation with a memory window size, L, according to the short memory
An Automated Lightweight UVM Tool
In this paper, an automated universal verification methodology (UVM) tool for rapid functional verification is presented. Now, UVM dominates the verification process but, it is very hard and too complicated to learn. This paper introduces a lightweight UVM tool which allows the user to rapidly verify complex RTL designs and different IPs. Also, it allows the user to perform the simulation for any design under test (DUT). The proposed tool generates the suitable UVM architecture to the DUT with the needed codes. Moreover, it provides the user with statistics about the number of the used classes

Double Visual Cryptography Using Generalized Tent Map, Rotation, and Image Filtering
This paper introduces a Multi-Visual Cryptography (MVC) system for sharing two color images, where the secrets can be revealed with low computation power using all the shares. The system uses the generalized Tent map as a source of randomness to generate any number of random shares. More specifically, (n-1) random shares are generated, and then, the nth share is calculated from the random shares and the secrets using rotations of the shares. In recovery, rotation of the last share recovers the two images based on the angle of rotation. Half the number of pixels is recovered for each secret

Battery Modeling with Mittag-Leffler Function
In various areas of life, rechargeable lithium-ion batteries are the technology of choice. Equivalent circuit models are utilized extensively in characterizing and modeling energy storage systems. In real-time applications, several generic-based battery models are created to simulate the battery's charging and discharging behavior more accurately. In this work, we present two generic battery models based on Mittag-Leffler function using a generic Standard battery model as a reference. These models are intended to fit the continuous discharging cycles of lithium-ion, Nickel-cadmium, and Nickel
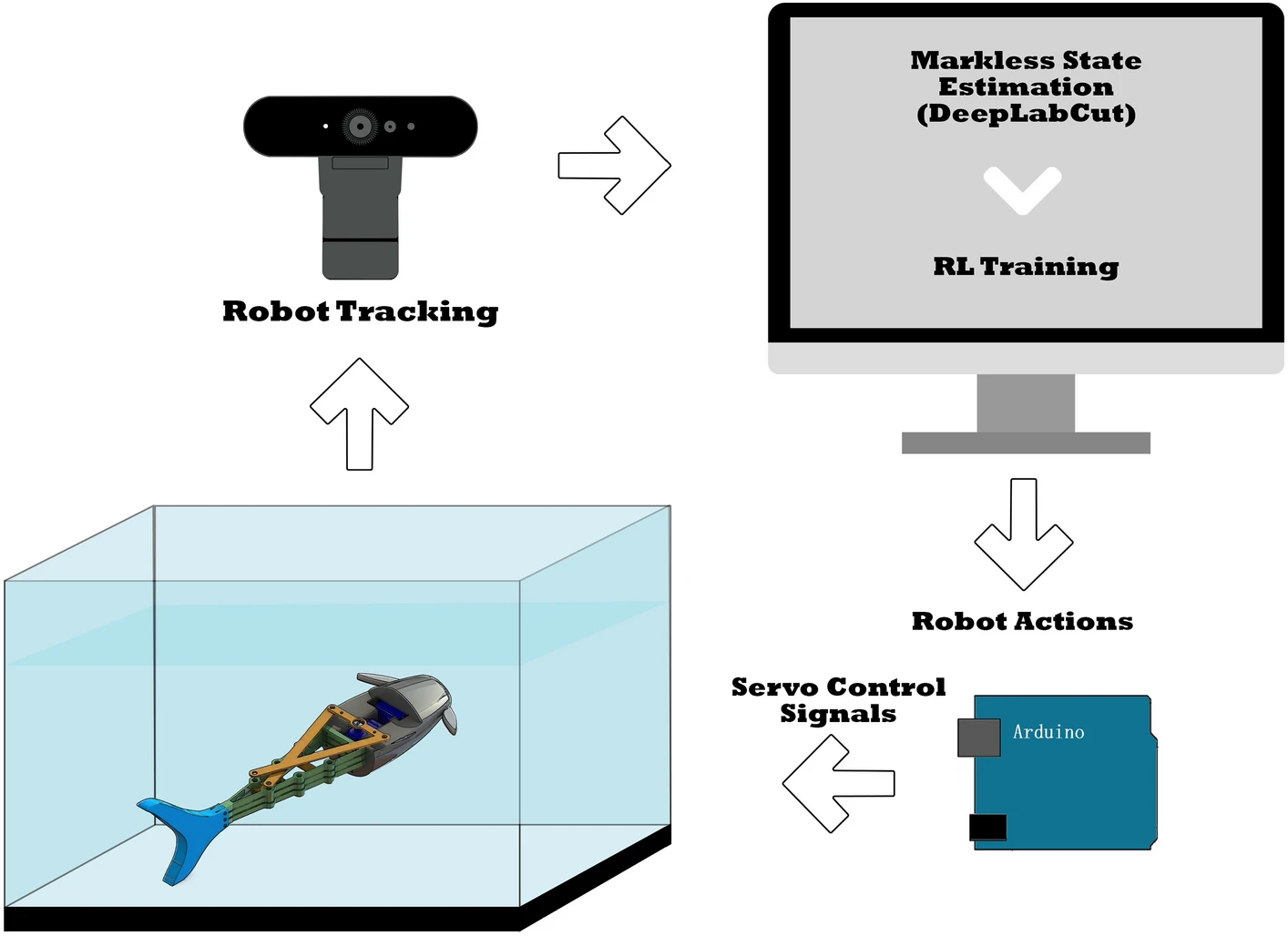
Design and control of soft biomimetic pangasius fish robot using fin ray effect and reinforcement learning
Soft robots provide a pathway to accurately mimic biological creatures and be integrated into their environment with minimal invasion or disruption to their ecosystem. These robots made from soft deforming materials possess structural properties and behaviors similar to the bodies and organs of living creatures. However, they are difficult to develop in terms of integrated actuation and sensing, accurate modeling, and precise control. This article presents a soft-rigid hybrid robotic fish inspired by the Pangasius fish. The robot employs a flexible fin ray tail structure driven by a servo
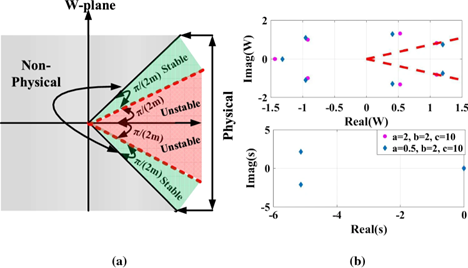
Correction to: Stability analysis of fractional-order Colpitts oscillators (Analog Integrated Circuits and Signal Processing, (2019), 101, 2, (267-279), 10.1007/s10470-019-01501-2)
Unfortunately, in the original version of the article some typos occurred. The typos have been corrected with this erratum. Below are the corrections:(Formula presented.). © 2019, Springer Science+Business Media, LLC, part of Springer Nature.
Pagination
- Previous page ‹‹
- Page 12
- Next page ››
