Breadcrumb
Design and fabrication of CNT/graphene-based polymer nanocomposite applications in nanosensors
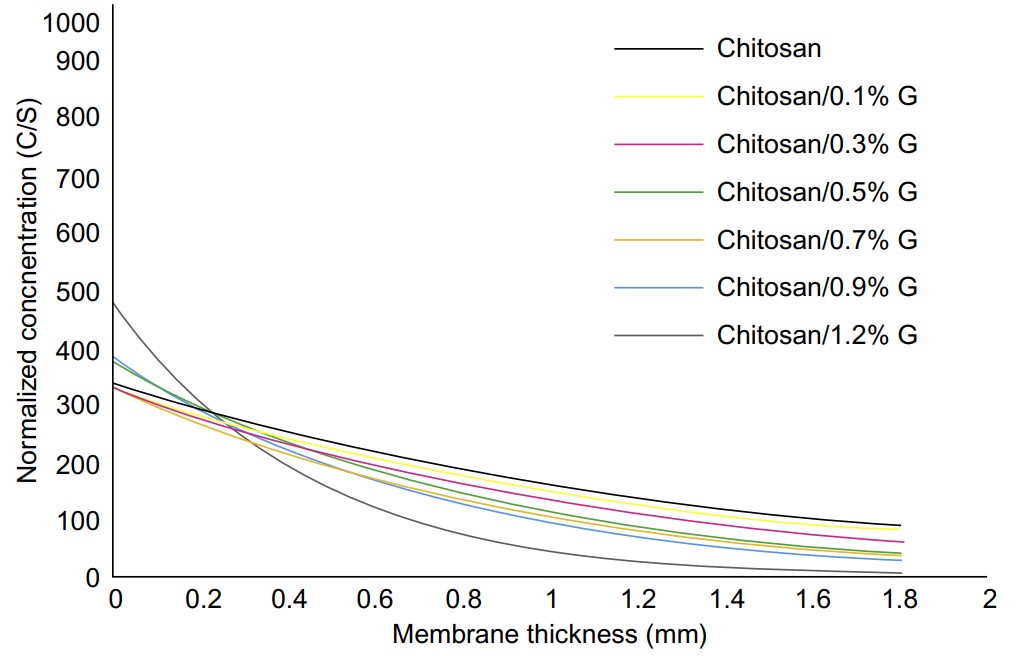
Development and improvement of nanosensors have been active research areas over the last few decades. Many materials and compounds have been investigated for their sensing properties. This work is concerned with developing a new sensing layer for gas sensors based on chitosan as a polymer enhanced with graphene as a nanofiller. The graphene used for preparing the chitosan solution was at 0.1, 0.5, and 1 wt%. Many characterizations (such as using different pore size, gas permeability, mechanical properties, and electrical resistance) were tested to give full insight into the nanocomposite
On the Approximation of Fractional-Order Circuit Design
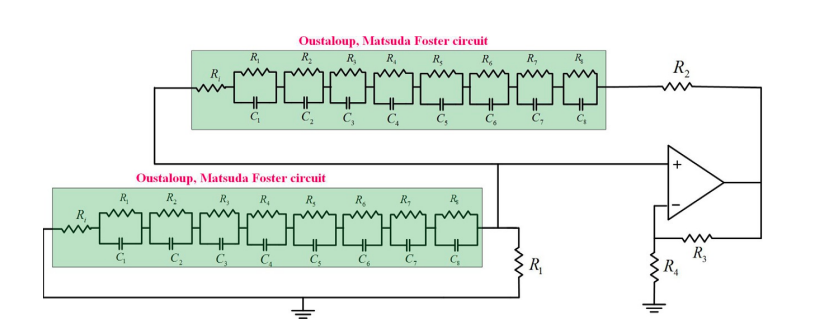
Despite the complex nature of fractional calculus, it is still fairly possible to reduce this complexity by using integer-order approximation. Each integer-order approximation has its own trade-offs from the complexity, sensitivity, and accuracy points of view. In this chapter, two different fractional-order electronic circuits are studied: the Wien oscillator and the CCII-based KHN filter with two different fractional elements of orders α and β. The investigation is concerned with changes in the response of these two circuits under two approximations: Oustaloup and Matsuda. A detailed review
Fractional-Order Filter Design
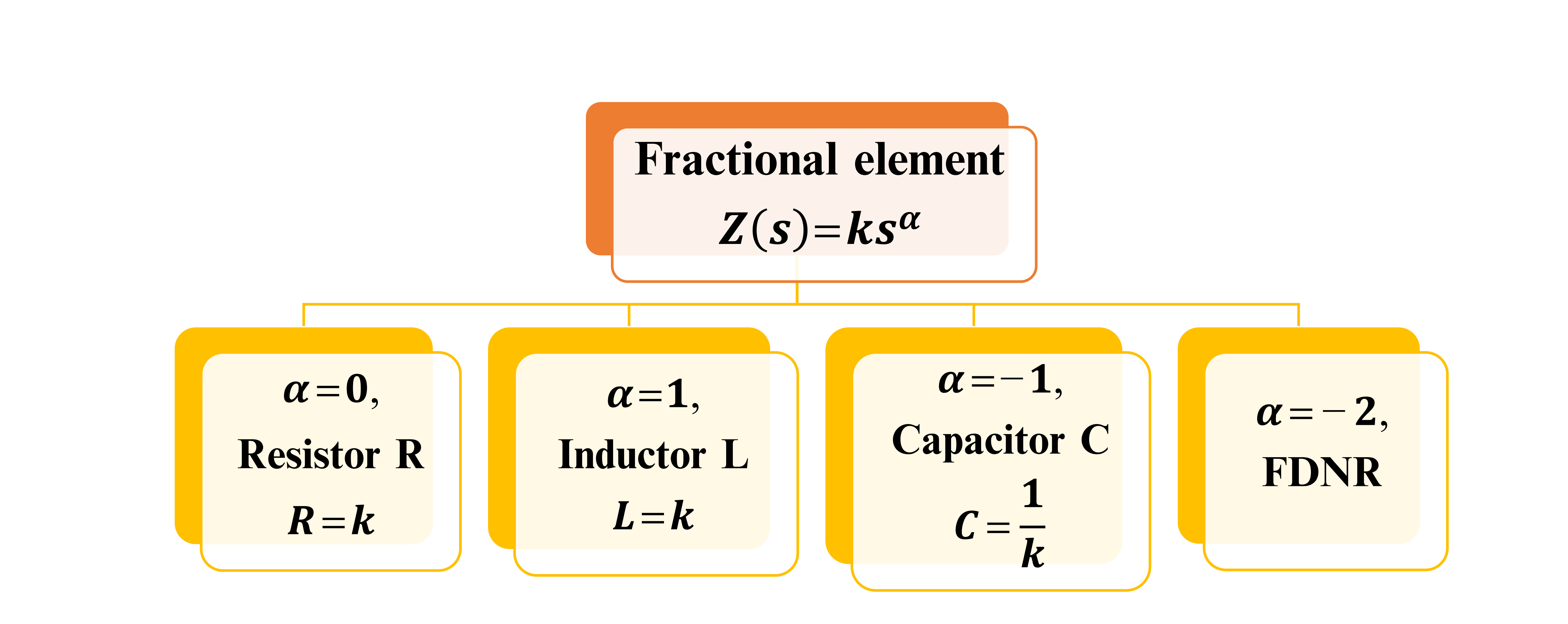
One of the advantages of fractional order is the extra degree of freedom added by the fractional-order parameters, which enrich the analysis with more details in new dimensions. This chapter introduces factional-order conventional filters of orders α, 2α, and 3α. The general transfer functions of continuous-time filters (low-pass, high-pass, and band-pass filters) to the noninteger-order (fractional-order) domain are investigated. Also, mathematical expressions for the maximum and minimum frequencies, the half power frequencies, and the right-phase frequencies are derived. In addition, the
Deep Neural Networks-Based Weight Approximation and Computation Reuse for 2-D Image Classification
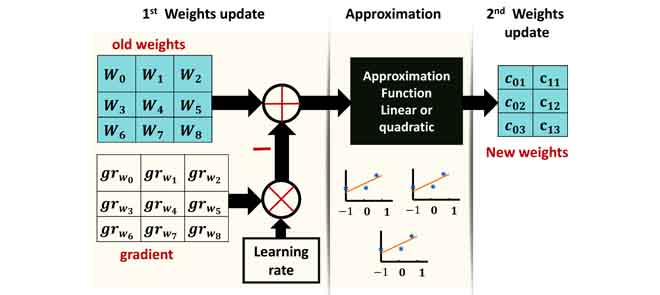
Deep Neural Networks (DNNs) are computationally and memory intensive, which present a big challenge for hardware, especially for resource-constrained devices such as Internet-of-Things (IoT) nodes. This paper introduces a new method to improve DNNs performance by fusing approximate computing with data reuse techniques for image recognition applications. First, starting from the pre-Trained network, then the DNNs weights are approximated based on the linear and quadratic approximation methods during the retraining phase to reduce the DNN model size and number of arithmetic operations. Then, the

CNTFET-based ternary address decoder design
With the end of Moore's law, new paradigms are investigated for more scalable computing systems. One of the promising directions is to examine the data representation toward higher data density per hardware element. Multiple valued logic (MVL) emerged as a promising system due to its advantages over binary data representation. MVL offers higher information processing within the same number of digits when compared with binary systems. Accessing memory is considered one of the most power- and time-consuming instructions within a microprocessor. In the quest for building an entire ternary
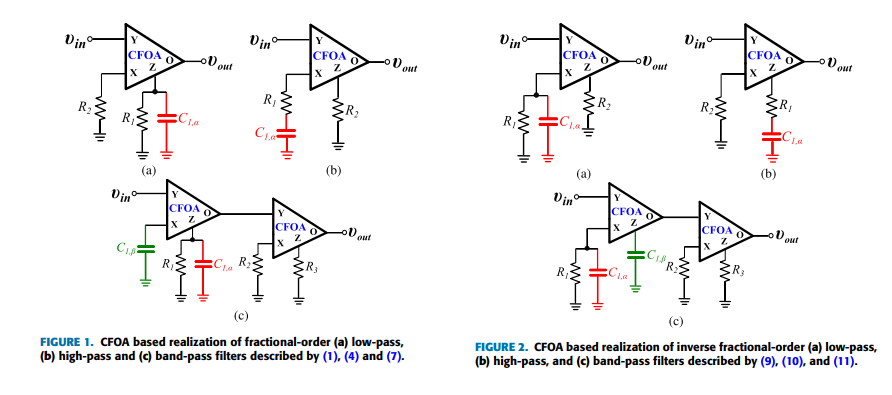
Non-Integer Order Generalized Filters Designs
Non-integer order filters can be derived from a generalized structure presented in this work. More specifically, fractional-order and power-law filters of single- or double-order are special cases of non-integer order filters with three degrees of freedom and can be implemented using a Current Feedback Operational Amplifier as the active element. The transfer function is formed as a ratio of two impedances which can be synthesized using Foster or Cauer RC networks. A curve-fitting based technique is employed for approximating the magnitude and phase of each impedance. The behavior of the
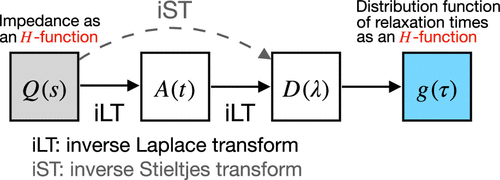
Procedure for Obtaining the Analytical Distribution Function of Relaxation Times for the Analysis of Impedance Spectra Using the Fox H-Function
The interpretation of electrochemical impedance spectroscopy data by fitting them to equivalent circuit models has been a standard method of analysis in electrochemistry. However, the inversion of the data from the frequency domain to a distribution function of relaxation times (DFRT) has gained considerable attention for impedance data analysis as it can reveal more detailed information about the underlying electrochemical processes without requiring a priori knowledge. The primary purpose of this paper is to provide a general and practical procedure for obtaining analytically the DFRT from
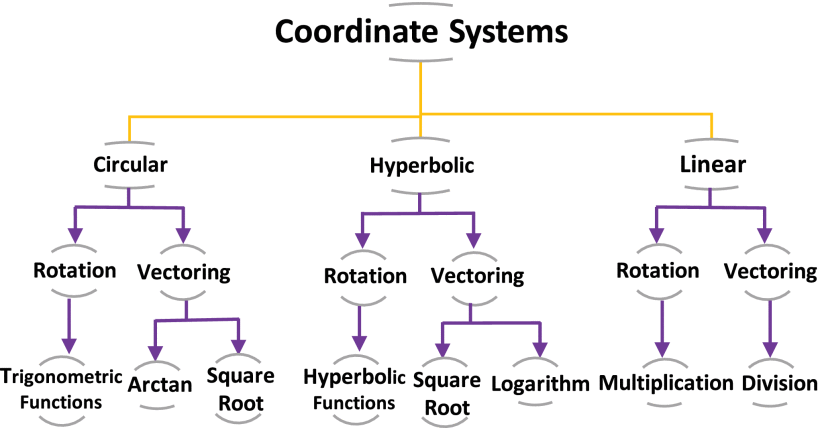
FPGA Implementation of Reconfigurable CORDIC Algorithm and a Memristive Chaotic System with Transcendental Nonlinearities
Coordinate Rotation Digital Computer (CORDIC) is a robust iterative algorithm that computes many transcendental mathematical functions. This paper proposes a reconfigurable CORDIC hardware design and FPGA realization that includes all possible configurations of the CORDIC algorithm. The proposed architecture is introduced in two approaches: multiplier-less and single multiplier approaches, each with its advantages. Compared to recent related works, the proposed implementation overpasses them in the included number of configurations. Additionally, it demonstrates efficient hardware utilization
On the fractional order generalized discrete maps
Chaos theory describes the dynamical systems which exhibit unpredictable, yet deterministic, behavior. Chaotic systems have a remarkable importance in both modeling and information processing in many fields. Fractional calculus has also become a powerful tool in describing the dynamics of complex systems such as fractional order (FO) chaotic systems. The FO parameter adds extra degrees of freedom which increases the design flexibility and adds more control on the design. The extra parameters increase the chaotic range. This chapter provides a review of several generalized discrete time one
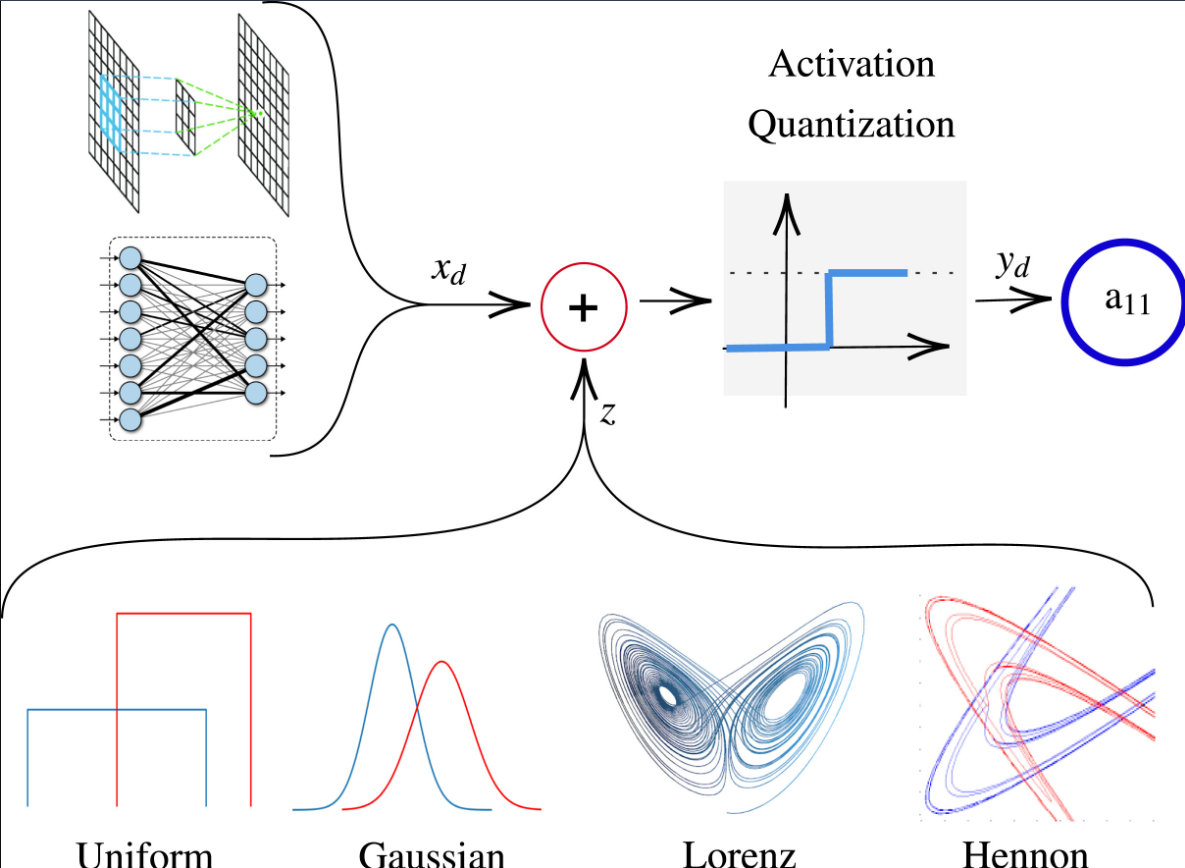
Chaotic neural network quantization and its robustness against adversarial attacks
Achieving robustness against adversarial attacks while maintaining high accuracy remains a critical challenge in neural networks. Parameter quantization is one of the main approaches used to compress deep neural networks to have less inference time and less storage memory size. However, quantization causes severe degradation in accuracy and consequently in model robustness. This work investigates the efficacy of stochastic quantization to enhance robustness and accuracy. Noise injection during quantization is explored to understand the impact of noise types and magnitudes on model performance
Pagination
- Previous page ‹‹
- Page 16
- Next page ››
